角动量的引入能为中心力场的薛定谔方程求解带来哪些帮助？为什么氢原子的角动量是量子化的？5月22日12时，《张朝阳的物理课》第五十六期开播，搜狐创始人、董事局主席兼CEO张朝阳坐镇搜狐视频直播间，先为网友们科普了矩阵力学和波动力学的历史，然后接着上一次直播课程的内容，继续讲解中心力场的薛定谔方程求解。在角动量平方与哈密顿算符的可对易性的指引下，成功将中心力场的薛定谔方程分离变量，得到径向方程和角向方程两部分。在这次直播课中，张朝阳把注意力集中在了角向方程上，证明了角动量是量子化的。

复习球坐标下的哈密顿算符 分离变量简化方程求解

氢原子的求解在之前的课程中已经涉及过，但很多步骤没有细讲，本节课程将会细致地介绍氢原子及相关的中心力场问题的求解。

张朝阳介绍，量子力学在发展之初，物理学家主要分成了两派。以薛定谔为主的一派建立了波动力学，通过波动方程描述量子力学中粒子的演化过程。以海森堡为主的一派建立的是矩阵力学。矩阵力学以描述算符为主，涉及的数学概念较多，而波动力学有经典的机械波理论与其对应，能给人们带来更直观的感受。

这两个理论表面上看起来非常不一样，但在后来被证明是等价的。如果把量子力学的建立看作是人类攀登一座高峰，那么矩阵力学和波动力学则对应着两条不同的爬山路径。无论选择从哪条路径出发，都能抵达量子力学的顶峰。

回到这次直播课程的主题上来。张朝阳带着网友们先复习了上一次直播课程的主要结果。对于像氢原子这类二体问题，它的哈密顿算符可以分解为质心运动部分与相对运动部分：

质心运动部分是简单的自由运动，而系统的主要特征包含在了相对运动部分中。因此，可以直接忽略质心运动部分，通过求解相对运动部分的方程来获得系统的主要物理性质。为了表述简便，下文忽略相对运动的rel下标，涉及的物理量特指与相对运动有关的物理量。

在球坐标下，中心力场的薛定谔方程为：

其中K_r为一个简记符号，代表哈密顿算符中与r的偏导数有关的项。由于角动量平方只包含了角度变量，因此它与K_r+u(r)对易。又因为一个算符与它自身对易，所以可以知道角动量平方算符与哈密顿算符对易。

在上一次直播课中，已经得到了z轴方向的角动量算符Lz与角动量平方算符、哈密顿算符都对易。这三个算符组成一个对易算符集。由于两个算符对易，必然存在共同本征函数，因此一组与哈密顿算符对易的算符集，能够为人们求解量子力学问题提供指引。

比如在中心力场问题中，如果使用角动量平方与哈密顿算符的共同本征值，那么哈密顿方程中的角动量平方可以直接替换成相应的本征值，从而能够简化方程。不过，张朝阳此处的做法更进一步。由角动量平方这个算符只包含角度变量，虽然在哈密顿算符中角动量平方还需要除以一个与r有关的量，但是实际上整个薛定谔方程是变量分离的。

为了突出这一点，可以把波函数表示为变量分离的形式：

由于K_r只包含对r的偏导数，因此上式第一项中的ψ_{θΦ}可以移到K_r的左边；同样，因为L^2只包含角度的偏导数，因此ψ_r可以移到L^2的左边。之后，等式两边同时除以整个波函数，并乘以r^2可得：

在直角坐标系下，L^2是三个方向的角动量分量的平方和，每个角动量分量都是厄密算符，其本征值必然是实数，因此各个角动量分量的平方的本征值大于或等于0，从而是半正定算符。

三个半正定算符的和依然是半正定算符，所以L^2的特征值必然大于或等于0，换言之A^2大于或等于0，这就是把它设为A^2而不是A的原因。L^2的本征值大于或等于0这一点在物理上是很好理解的，因为从物理直觉上，角动量平方必然不是负值。

张朝阳用分离变量法处理薛定谔方程

波函数连续单值可归一 观测量离散多值量子化

径向方程与A^2有关，而A^2是L^2的本征值，因此需要先求解角向方程才能完整求解径向方程。所以，在这一次直播课把精力集中在了角向方程上，径向方程将留到后续课程中求解。

张朝阳沿用物理学中的习惯，把A^2表示成了l(l+1) ћ^2，其中l为非负常数，ћ^2出现在这里是为了平衡量纲，因为角动量平方与ћ^2的量纲一致。由于A^2大于或等于0，所以无论A^2的值是多大，必然存在且只存在一个非负的l满足l(l+1) ћ^2=A^2。在l的表示下，角向方程可以写为：

张朝阳强调了这个解与平面波的区别。平面波方程的自变量取值范围是从负无穷到正无穷，但是角度Φ的取值范围是0到2π。考虑到波函数要满足单值性的要求，角度0和角度2π的波函数必须相等，也就是：

所以m只能取整数值。这是氢原子角动量的第一个量子化条件，表示氢原子沿z轴方向的角动量只能取ћ的整数倍。注意，这个量子化条件来自于波函数的单值性要求。

综合上述讨论，可以得到：

张朝阳推导得到连带勒让德方程

这正是著名的(连带)勒让德方程，对不同的m与l，它的解被记为：

相应的勒让德方程为：

由于零不能作为分母，所以上式不适用于某个a_k等于0的情况。如果某个a_k=0，根据递推关系容易得知，当n>k时都有a_n=0，也就是说这个无穷级数是截断的，它实际上是个多项式。

如果所有a_k都不等于0呢？根据上式可知：

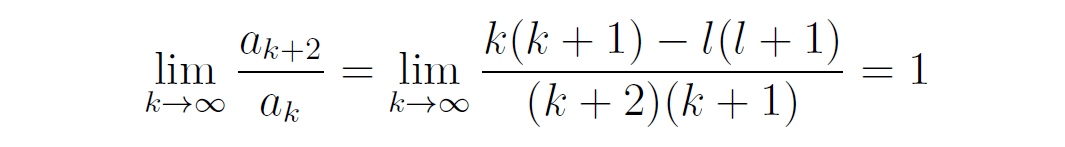
根据这个条件可以证明P_l(x)趋向于1时是发散的。这不满足前文所说的波函数的连续性条件。因此，必然存在某个a_k=0，从而P_l(x)截断成为一个多项式。

什么情况下才会存在某个a_k等于0呢？张朝阳提示网友们观察前面的式子，如果k(k+1)=l(l+1)，那么a_{k+2}就等于0了。考虑到l是非负的，k是自然数，故l=k也是一个自然数。这个分析可以倒退回去，如果l是一个自然数，那么a_{l+2}必然等于0，所以上述无穷级数截断为一个多项式。加上l取0的情况，最终，为了满足波函数连续性的要求，l只能取非负整数值。

张朝阳介绍l的量子化来源

推导到这里，一共出现了两个量子化的数，一个是m，只能取整数值；另一个是l，当m=0时l只能取非负整数值。其中，m的量子化来源于波函数的单值性要求，l的量子化来源于波函数的连续性要求。波函数需要满足连续单值可归一的条件，连续与单值在这里都已涉及，那可归一的性质呢？它将会在求解径向方程时体现出来。